J'ai déjà fait part de mon idée de quitter ce monde en 2025, année sympa car 2025 carré de 45, valeur de "Rémi" comme de "carré".
J'aurai 75 ans le 6/7/2025, 2025 multiple de 75, de même que 1950, mon année de naissance.
J'ai envisagé la date du 26/7, où Jung aurait 150 ans.
, "quatre" en hébreu, m'a conduit à calculer que le dernier jour de 2025 serait le 27573e de mon existence, 27573 produit de 101 par 273. Sympa encore, car 31/12 c'est 21/13 à rebours.
Quelques problèmes de santé motivaient ma décision, et ma vie n'était pas très marrante depuis la mort d'Anne le 13 février 21 (et avant avec sa maladie c'était pas spécialement le pied tous les jours).
Peu après le 4e anniversaire de sa mort, le principal problème, non identifié par les allopathes, est revenu, avec une acuité telle qu'il m'a fallu recourir au fentanyl conservé depuis 4 ans.
Il m'a semblé devoir réviser mes calculs, et je me suis aperçu que le 2 avril serait le 27300e jour de mon existence. Avec l'histoire des intervalles, le 3 avril survient 27300 jours après ma naissance, et, du 3/4 16:45 jusqu'au 4/4 16:44 ma vie contiendrait 27300 jours (périodes de 24 h) et des poussières.
. J'ai créé ensuite le billet 443, commencé à l'écrire, et constaté que son PostId (identifiant propre à chaque billet, était
débutant par 444. J'ai donc créé un autre billet, et réservé ce numéro pour le 444e billet, à publier idéalement le 4/4, mais j'envisageais d'autres publications avant l'aggravation de mon état...
La donne a changé avec le problème de santé qui semble si sérieux que je ne sais si je vais tenir jusque là. D'autres calculs m'ont amené d'autres découvertes.
Le 4/4 est le 273e jour à partir du 6/7 de l'année précédente, inclus ou non selon que l'année en cours est banale ou bissextile.
Le 4/4 à venir sera le 1512e jour à compter depuis celui, inclus, de la mort d'Anne. 15 et 12 sont dans le rapport 5/4, quintessence et quaternité. Lors de la création de
, j'ai trouvé significatif que son BlogId (identifiant du blog, figurant avant le PostId, accessible par le champ "commentaires" au bas du billet) débute par les chiffres 8064, avec de même 80/64 = 5/4.
, dont les 4 premiers tomes ont 64 pages, le 5e et dernier, 80.
1512 et 8064 sont des multiples de 168, le nombre de pieds d'un sonnet d'alexandrins, forme poétique que j'utilise fréquemment.
Il m'est venu d'écrire un sonnet en 168 lettres de valeur 1512, et un autre en alexandrins, débutant par "1512", puis 504 lettres de valeur 6552.
et je le poste illico, avant de partir pour l'hosto. J'y reviendrai si je survis...
Le dernier vers a 5 pieds, c'est voulu.
La fin du 9e vers, "quatre", correspond à la valeur 936, 13 fois 72. La valeur totale 1512= 21 fois 72. Un autre 13/21, non prémédité... Les 5 derniers vers, 576= 8 fois 72, ou carré de 24.
, répartie en 1512 et 6552, produit des Fibos 3.8.13.21. Du temps où je choisissais des heures de publication significatives des billets, en essayant d'y associer des PostId en rapport, j'avais choisi pour heure de publication du billet consacré à mon 60e anniversaire l'heure 06:07 et un PostId asssocié finissant par 65526552. C'est détaillé
.
1er mars. Je reviens à ce post 444, après avoir publié une 1e version, inachevée du post 443. Pour l'heure il me semble plus important de partager quelques constatations.
Je renonce à l'idée énoncée ci -dessus d'écrire le sonnet 1612+6552. J'en serais peut-être encore capable mais ça n'aurait sans doute que peu d'intérêt.
Alors voici ce qui me semble importemps, bien que je me sente incapable en mon état actuel de l'expliciter.
, survenue à cette demoiselle le 4 avril 1959, selon R. de Warren (1981), et de la nom moins bizarre histoire de
arrivée ce même 4 avril 1959, selon la nouvelle éponyme de Philippe Claudel (2003).
Outre qu'il s'agit chaque fois d'une fille au nom slave associée au nombre 56(-)91 perdant son pucelage le 4/4/59, d'autres points communs sont apparus
, comme ces illustrations de Burne-Jones en couverture, avec probablement le même modèle,
Peut-être Warren a-t-il voyagé dans le temps, puisque c'est un thème de son roman, et a-t-il ramené du futur un souvenir de Claudel, mais je suis à ce point certain que Claudel n'a jamais lu une ligne de Warren qu'il ne m'est jamais venu à l'idée d'essayer de le contacter. Une autre curiosité est que j'ai été conduit à lire cette nouvelle, car l'auteur est on ne peut plus éloigné de mes intérêts littéraires.
C'est ce que j'appelle, et j'en décide ainsi aujourd'hui, un "merle or". J'avais d'abord opté pour merle blanc, mais, quoique rares, il y a des merles blancs, alors que le merle or semble inconnu de l'ichtyologie.
Si mes facultés intellectuelles me semblent avoir fortement régressé, je connais des gens, certains étant de chers amis, dont je sais que le ciboulot est bien meilleur que ce qu'a jamais été le mien. Pourtant, si je leur parle de ce "merle d'or" par exemple, ils ne veulent pas en entendre parler, parce que les merles d'or ça n'existe pas, donc je me goure forcément.
Ou alors on fait appel à la loi des grands nombres. Il y a tellement de faits qu'il existe forcément des coïncidences. Je connais des tas d'autres merles d'or, qu'à cela ne tienne, il n'y a pas de limite à la loi des grands nombres puisque les cas sont infinis...
Et puis mes merles d'or font souvent appel à des connaissances particulières, et "je ne peux pas en juger, car je ne suis pas latiniste-hébraïsant-musicologue-arithmomancien-etc. (rayer les mentions inutiles)". Mais il existe des spécialistes de toutes ces matières.
Et puis moi je connais des dizaines, des centaines peut-être, de merles d'or, que je ne peux tous considérer dans leur globalité, car selon Daumal on ne peut appréhender plus de 5 choses à la fois, mais je pourrais au moins les lister, alors que tout autre est contraint d'étudier laborieusement tel ou tel cas, puis de passer à tel ou tel autre.
Et puis il y a les métadonnées...Je ne sais trop ce que ce mot signifie exactement, mais il dénote ici ma certitude qu'on ne peut isoler un merle d'or du reste de la volière. Il existe, il doit exister, une image dans le tapis, quelque chose qui rende compte de l'ensemble du phénomène. Après y avoir été confronté depuis près de 40 ans, j'ai quelques idées, purement empiriques, mais il me semble prématuré d'en faire part à qui récuse le phénomène.
Il y aurait aussi le zarbi, mais le zarbi se caractérise essentiellement par sa non-répétitivité, sinon ce ne serait plus du zarbi. Alors qu'en principe, pour mon exemple, chaque lecteur de verra perdre son berlingot le 4/4/1959, l'une ayant la gématrie 56 91, l'autre recevant le numéro 5691.
Pour les cupides, il serait envisageable de se faire des burnes en or en abordant le phénomène de façon commerciale...
Voici ce qui m'a retenu en relisant Sloty 1959 du 4/4/11.J'y avais été amené à découper les noms de nos saisons en 8 syllabes, selon l'ordre usuel :
hi17 ver45 prin[119]57 [119]
temps[192]73 [73]
é5 té25 au22 tomne67 [119]
[Ce texte de 24 lettres a une somme gématrique de 311.]
- 02 -
2 mars. Une nuit de passée, difficile... Je me borne à une petite anecdote. Les docteurs demandaient souvent à Anne, Sur une échelle de 1 à 10, à combien évaluez-vous votre douleur?
"200" lui arrivait-il de répondre.
Le passage au Gématron supra montrait donc une double césure d'or des 8 syllabes saisonnières en 3-1-4, avec au centre TEMPS = 73, une syllabe qui est aussi un mot, et un mot qui n'est pas sans rapport avec l'année.
Je donnais quelques échos dans ce billet Sloty 1959, mais avais aussi en tête une comparaison ultérieure avec l'ode Toi l'été composée en 1999 pour mon roman Sous les pans du bizarre, se présentant ainsi dans le premier jet:
Les 72 lettres de ce petit texte se sont ensuite miraculeusement adaptées à un prolongement utilisant les propriétés du nombre 365 ayant motivé le roman, puis encore plus miraculeusement à une harmonie bachienne. J'y suis souvent revenu, notamment en
.
La première syllabe HI de HIVER m'est devenue ensuite si significative que j'ai titré
un billet de 2022. Ceci est en relation avec le sonnet que j'avais codé dans le roman, une récriture des
de Rimbaud.
J'imaginais que c'était une innovation, mais j'appris plus tard que Jean Ricardou avait publié en 1972 un texte où était codée une récriture du
de Mallarmé. Le mot "hiver" était présent dans le sonnet de départ, et
La somme 311 pour les 4 saisons ne m'est guère évocatrice. Une
.
totalisent 311 lettres. Ces 311 lettres totalisent la valeur 3665.
La répartition en quatrains et tercets était importante chez Ricardou comme chez moi.
La valeur 73 de TEMPS m'est importante, parce que 5 fois 73 font 365, parce que le roman de Warren débute le 7/3 par un saut dans le temps, deux semaines avant l'équinoxe de printemps. Le saut suivant surviendra le 4/4, deux semaines après cette équinoxe.
La retrouvaille de cette syllabe centrale TEMPS m'a aussitôt évoqué la voix de Gilbert Bécaud:
. Je n'étais alors en rien fan de Bécaud, et n'appréciais guère cette chanson, mais j'ai un certain souvenir d'avoir été marqué par ce quintuplet.
C'est une curiosité d'avoir les noms des deux saisons où les jours croissent en rapport d'or avec ceux des deux autres saisons, où les jours décroissent. Sol invictus? Le symbole du soleil est aussi celui de l'or. [Ajout ultérieur: le numéro atomique de l'élément Au est 79, valeur du français "vérité". Dans le
Je remarque que 311 + 54 = 365 (54 valeur de JUIN, DEUX, VIER, par exemple).
Les saisons suivant les solstices sont HI-VER et E-TE, ce qui me fait penser au mot VERITE.
Si l'accent doit être mis sur le jour le plus long, à la "fin du printemps" (la faim des printemps), je souligne que
, "vérité", valeur qui m'occupe intensément depuis mai dernier, avec la série des Thilliez non-Sharko en 441 chapitres, et le rebond récent de la découverte des
- 56 91 - Or 441 c'est aussi 3 fois 147, MARINA SLOTY = 56 91, mais encore SINOUE HALTER, les deux auteurs qui ont joué un rôle certain dans ma découverte de l'harmonie de la vie de Jung autour du 4/4/44. Je rappelais dans le billet précité que les deux formules anagrammes trouvées dans
Alphabets de Perec,
Hélas ni route. et
Sait-on l'heure? donnaient
avec
Sinoué-Halter un autre 441.
Lors de ma découverte du PostId du projet de billet 443, 4440256918605723090, il m'a paru de l'immédiate évidence de l'utiliser pour le billet 444. J'y remarquai que 444(0) était suivi par 256, soit 4.4.4.4, or une
orthographe de l'autre protagoniste de l'échange du 4/4/44 est
"THEODOR HÄMMERLI-SCHINDLER" = 85+79+92 = 256.
Aujourd'hui 02 mars où je poursuis l'écriture de cet ultime billet, je m'avise que les chiffres suivant 56 sont 91, alors que je ne prévoyais nullement au départ d'y utiliser l'affaire Sloty. Je ne me rappelle en fait pas ce qui m'a conduit à relire ces billets et y retrouver l'équilibre oublié autour de (PRIN)TEMPS.
Il y a sans doute plus hallucinant. En prenant en compte le nom complet de Jung,
CARL GUSTAV JUNG = 34+90+52 = 176, l'addition à 256 donne 432, soit deux fois 216.
Une personne dont je me suis senti très proche en ce monde est Jean-Pierre Le Goff, obnubilé par le nombre 216. JPLG a fêté ses 21600 jours d'existence par un aller à Thoires (21), puis ses 21816 (101x216) par un aller à Thouars (79). Lorsque je lui ai fait part qu'un village proche de chez moi était Thoard (04), il a souhaité y intervenir, mais nous n'avons été que nous deux sur le coup.
La date de ses 102x216 jours était le 26/11/02, mais je ne me suis aperçu que bien plus tard de l'équivalence des chiffres, et ne sais s'il en était conscient.
Si j'arrive à tenir jusqu'au 4/4, et à publier ce jour le billet 444 achevé, peut-être aurai-je réussi à faire quelque chose en ce monde, avant d'en visiter quelques autres, je l'espère un peu moins tartes.
Il y eut un autre "
aller à Thoiry". Lorsque je remmenais JPLG à Aix-TGV le 27/11/02, en devisant sur le nombre d'or chez Perec, il me demanda soudain de m'arrêter, dans un coin nommé ravin de Laval. Il venait de voir un panneau
NOMBRE
D’OR au bord de la route, en pleine campagne, et c’était exact. Nous
devions découvrir par la suite qu’il s’agissait du nom d’une maison
cachée dans les arbres d’une colline dominant la route, baptisée
Ayguelune par son constructeur et récemment renommée
Nombre d’or par ses nouveaux propriétaires.
Je les ai rencontrés, Anette Prins et son mari Rein-Jan.
Prins-Printemps?
Le croira-t-on, j'ai jadis (1982) fait partie de la secte Ananda Marga où j'ai reçu le nouveau nom Ranjan, et j'ai publié une
nouvelle (2001) sous le pseudo Annette Devi.
J'avais oublié de me munir d'un décamètre lorsque j'ai visité les Prins, mais j'ai dénombré les planches de leur chalet, 56 en largeur, 91 en longueur. J'ai des photos qqpart, mais où?
JPLG a aussi lu
Marina Sloty, et fait une intervention sur les lieux (Larzac). J'en ai parlé qqpart, mais où?
- 86 -3 mars. Un 4/4 important a été le 4/4/2019 où j'ai publié
Quatre quarts au carré, Carl, 279e billet du blog.
Intermezzo: je consulte à 10:00 le tableau de bord du blog, affichant
Je n'avais signalé qu'à 2 personnes le billet 443, également inachevé.
Retour au billet du 4/4/19, consacré à à une ambitieuse création, la transformation du carré diabolique d'ordre 4 en 16 vers de 34 lettres, chaque vers de gématrie 408.
Il y avait deux versions du poème, l'une en 128 mots afin d'ajouter une nouvelle harmonie à ce niveau. Je ne suis pas mécontent de ces textes, bien qu'ils aient été réalisés en temps polynomial (soit "rapidement", c'est une expression de matheux).
Le dernier vers était dans les deux cas
"Apprend-on l'intérêt ?", rit la fille du Temps.
C'est une allusion à Rabelais:
la responce faicte
par le saige Taies à Amasis Roy des Egiptiens quant
par luy interrogé en quelle chose plus estoit de prudence, respondit : on temps. Car par temps ont esté & par temps seront toutes choses latentes inuentees & c’est la cause pourquoy les anciens ont appelle
Saturne le Temps, père de Vérité, & Vérité fille eut
Temps.
Ce n'est plus le moment de me livrer à une exégèse. Qu'on sache qu'il y a 30 ans j'ai écrit au moins deux études sur Rabelais,
Eléments pour une gématrie rabelaisienne, que Noël Arnaud souhaitait publier, mais je venais alors de découvrir
Vocalisations de Perec, et ne pensais plus qu'à ça.
Une autre étude était
La langue hagarène, que j'ai égarée. Selon Rabelais, le nom Pantagruel vient du grec
panta-, "tout", et de l'hagarène
gruel, "altéré".
Hagar est le nom de la servante d'Abraham, la mère d'Ismaël. En hébreu, ça s'écrit en 3 lettres H-GR, et se traduit "L'Etrangère". Les 2 lettres GR,
Gimel-Resh, formant le mot "étranger", sont un couple atbash : G est la 3e lettre à partir du début de l'alphabet, R la 3e lettre à partir de sa fin. Ce code
atbash est employé dans la Bible, et il intervient souvent dans mes analyses.
Le point de départ de mon étude était que, dans l'alphabet rabelaisien, c'est-à-dire l'alphabet latin, GR sont aussi un couple atbash : G est la 7e lettre à partir du début de l'alphabet, R la 7e lettre à partir de sa fin. C'est plutôt inattendu. Tout ce dont je me souviens de cette étude est que
V E R I T E = 20 5 17 9 19 5 = 75 (alphabet latin), donne l'atbash
D T G P E T= 4 19 7 15 5 19 = 69, tandis que
T E M P S = 19 5 12 15 18 = 69.
VERITE fille eut TEMPS ?
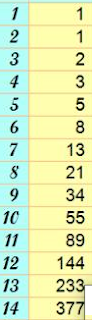
Je rappelle que j'ai une approche valériano-ricardolienne de la littérature, sinon de la vie en général. Lorsque Marina Sloty (56 + 91 = 147, multiples des Fibos 8-13-21) fait un saut temporel de 89 ans vers l'an 1870 = 34x55, 34-55-89 Fibos suivants, dans un roman dont le titre vaut 377, 144-233-377 Fibos suivants, pour moi ça veut dire que Fibo est concerné, même si l'auteur n'en avait aucune conscience.
J'ajoute que j'ai hésité plus haut à donner la valeur de la chanson de Bécaud,
Un peu d'amour et d'amitié = 235, m'évoquant 2-3-5, les Fibos précédant 8-13-21, et voici que la Wikisource de "VERITE fille eut TEMPS" est une
page 235.
Je reviens aux deux poèmes s'achevant sur
"Apprend-on l'intérêt ?", rit la fille du Temps.
Ils illustrent le carré diabolique ou pandiagonal d'ordre 4, connu depuis près de 10 siècles en Inde, où il figure sur un
pilier du temple de Khajuraho, les chiffres indiens correspondant à
7 12 1 14
2 13 8 11
16 3 10 5
9 6 15 4 La découverte des partages verticaux 13-21 du carré de Dürer
m'avait conduit en
2010 à cette représentation, songeant que les 4-4-4-4 nombres du carré ont pour somme 136, correspondant à
JUNG HAEMMERLI = 52+84
avec 52/84 = 13/21, le même partage apparaissant pour les lettres paires et impaires de CARL.
Le carré diabolique a apporté d'autres corrélations. C'est ainsi que parmi les 1820 combinaisons de 4 nombres parmi les 16 premiers, il y en a 86 offrant la constante magique 34, 86 valeur de CARL JUNG (et 34 valeur de CARL).
Et parmi ces 86, seules 52 (JUNG) sont "logiques", se déduisant par d'immédiates symétries dans le carré diabolique.
Je ne reviens pas sur le nombre 1768 évoquant les 68 et 17 ans de Jung autour du 4/4/44, car le PostId 4440256918605723090 ne semble pas avoir encore livré toutes ses possibilités.
J'ai donc isolé 444, puis 02 pour ma découverte du 2 mars, puis 5691. Viendrait maintenant 86, pour CARL JUNG par exemple, mais aussi pour MERLE OR, l'expression que j'ai forgée pour désigner l'oiseau rare, l'oiseau impossible plutôt, or
MERLE OR = 53 33, partage doré entier idéal de 86.
Il me semble que "merle or" pouvait se justifier à partir de "merle blanc", mais je peux tout à fait envisager que mon esprit familier de ces calculs soit capable de forger de telles harmonies sans en informer ma conscience. Je rappelle au passage que
sloty signifie "or".
Mais il y a davantage, et du lourd, difficilement attribuable à mes neurones cacochymes.
J'ai été amené à forger l'idée de séries additives conjuguées. J'imagine que ça a été vu ailleurs, mais je ne suis pas matheux, juste amatheur, alors je ne sais où chercher confirmation.
Il y a ainsi par exemple la fameuse suite Fibo, 0-1-1-2-3-5-8..., dont la conjuguée est la suite de Lucas, 1-3-4-7-11..., ou (0+1)-(1+2)-(1+3)-(2+5)-(3+8)... Ces nombres de Lucas sont dans un rapport proche de racine de 5 avec les nombres de Fibo, et réitérer les opérations conduit à 5 fois la suite Fibo, puis 5 fois la suite Lucas, 25 fois la suite Fibo...
Alors 33-53 fait partie de la suite
22096,
1-6-7-13-20-33-53-86...
incidemment mentionnée par Perec dans
"53 jours", mais l'absolument éplapourdissant (ça fait longtemps que je l'avais pas ressorti), c'est que la conjuguée de cette suite 22096 est la suite
206420,
8-19-27-46-73-119-192-311...
précisément la suite saisonnière vue plus haut, que je propose de baptiser
resurgissement solsticial
car
resurgissement solsticial = 192 119, de même que
(HIVER PRINTEMPS) (ETE AUTOMNE) = 192 119
en rapport d'or optimal 192/119 = 1,613...
192 = 3 fois 64, valeur de ZERO. J'ai une vague réminiscence de
Corsaire Triplex de Paul d'Ivoi ou le triple zéro jouait un rôle.
4 mars.
En fait, tout simplement,
CORSAIRE TRIPLEX = 192, mais il y avait autre chose, probablement paumé dans un vieil ordi. Une curiosité associée était que le roman avait une suite,
La capitaine Nilia, et qu'un chapitre entier avait été oublié dans l'édition en LP, rendant le roman incompréhensible. [Ajout ultérieur: cette NILIA me fait penser maintenant au kernos de MILIA, trouvé en Egypte, M et N couple central de l'alphabet utilisé en conscience par Lahougue]
La
vérification au Gématron de
resurgissement solsticialhiverprintemps étéautomneamène à constater, outre les égalités 14+10 lettres, que la petite section d'or, sous cette forme, tombe exactement après SOL:
L'équilibre doré des paires de saisons séparées par les solstices m'avait fait évoquer plus haut le fameux
Sol invictus, le Soleil invaincu, principale fête des Romains, remplacée par la naissance du Christ pour la faire oublier. De même on a fait correspondre le Baptiste à l'autre solstice (Il faut que Jean décroisse pour que Jésus croasse...)
Tiens, selon l'alphabet latin,
sol invictus = antichristus = 154,
valeur de FRANCK THILLIEZ selon notre alphabet.
L'apparition gématronique de 238 et 119 m'évoque de nouveaux
liens entre lumière et vérité, Lux & Veritas, ourim we-thoumim...
L'oracle utilise traditionnellement les noms des fils de Jacob, j'en ai traité
ici.
Rachel (RHL=238) a d'abord baptisé son dernier fils BNAWNY = 119 (fils de ma douleur) avant que Jacob (YOQB = 182) ne le renomme Benjamin.
Tous des multiples de 7, et Jacob vit 147 ans, 3 fois 147 = 441,
emeth, vérité.
Mais mieux vaut ne pas partir dans trop d'hébraïsme, je crains que tout le monde ne suive pas...
Lorsque j'ai redécouvert le 311 des 4 saisons, j'ai aussitôt pensé au nombre 113, dont j'ai souvent parlé, et qui faisait précisément l'objet d'une compilation en préparation.
Il se trouve que les jeux 56-91 et 5691 commandaient de revenir sur les OMSOS (
OrthoMagic Squares Of Squares) où ces nombres étaient plutôt miraculeusement apparus, et je me suis avisé que j'avais abordé la question dans le
billet 113 de
Quaternité, pas par hasard car le billet précédent était
consacré à ma seconde anagramme de
Vocalisations, en 112 mots, avec carré orthomagique intégré...
5 mars
Les OMSOS (
OrthoMagic Squares Of Squares) sont formés de termes
qui sont eux-mêmes des carrés. Kevin Brown a étudié les carrés d'ordre 3
de constante inférieure à 30000, et a découvert
91 carrés primaires,
parmi lesquels la constante est dans
56 cas un carré.
C'est assez étonnant en soi, mais Brown semble plus intéressé
par le fait que le premier OMSOS dans la série des 35 autres (dont la
constante n'est pas un carré) soit formé de carrés de nombres tous
premiers.
Et cette constante est 5691.
Certes, MARINA SLOTY, c'est
56 + 91, alors qu'il y a ici
91 OMSOS dont
56 avec une constante carrée (mais SLOTY peut se répartir en LYS =
56 et TO = 35).
Je remarque que les rangées de nombres à la puissance 1 totalisent 105-119-121, 3 fois 115, les colonnes 115-123-107, 3 fois 115 (
ET LE TEMPS). Ou encore 2 fois 345, ce qui me rappelle une
découverte associée à une synchronicité (à noter dans ce post une référence 235 à l'atbash).
Il y a 6 autres sommes de 3 carrés totalisant la constante
5691, 29-37-59 (premiers), 1-47-59, 25-29-65, 19-29-67 (premiers), 5-25-71, et 1-19-73.
Des prolongements sur le
billet 113 où j'explorais les OSMOS d'ordre 4.
6 mars
Le
billet 112 précédent était donc consacré à une nouvelle anagramme de
Vocalisations, construite autour d'un carré orthomagique à partir des 16 premières consonnes, de constante 45 donc. Je rappelle que nous sommes en 2025 = 45x45.
Il semble que ma prognose soit plus favorable, et que j'aie des chances d'atteindre le 4 avril, au moins.
Le sonnet du billet 112 citait CARL (Jung) et ARMIN, le frère de Theodor Haemmerli, le médecin qui avait guéri Jung, tombé malade le 4/4/44, au début de la convalescence de Jung, et mort le 30 juin suivant, au moment où Jung quittait l'hôpital.
J'ai cité
ici l'intégralité d'une lettre de Carl à Armin en soulignant
CARL JUNG = 34+52 = 86 avec
ARMIN HAEMMERLI = 55+84 = 139.
Chaque élément du premier nom est en rapport d'or avec l'élément
correspondant du second. Il a été vu que 52 et 84 sont les quadruples de
13 et 21, termes de la suite de Fibonacci qui se poursuit précisément
par 34 et 55, CARL et ARMIN...
Ainsi chacun des deux noms peut correspondre d'une certaine manière à un motif quintessentiel 1+4.
Aujourd'hui, je remarque que 86 et 139 sont des nombres de la suite 22096, dont la suite conjuguée est la suite
206420,
8-19-27-46-73-119-192-311...
précisément la suite saisonnière vue plus haut, que j'ai proposé de baptiser
resurgissement solsticial,
en pensant au
Sol Invictus, et à l'harmonie dorée des deux paires de saisons autour des solstices. Il n'y a pas adéquation entre ces paires de saisons et les semestres (Haemmerli est mort le jour même de la fin du premier semestre), probablement à la,suite d'erreurs impossibles à corriger ensuite. Même la naissance de Jésus ne coïncide pas exactement avec le solstice.
Et évidemment ARMIN - MARINA (Sloty).
7 mars, Perec aurait 89 ans.
Après [56 91] du PostId évoquant MARINA SLOTY, j'ai vu [86] pouvoir correspondre à MERLE OR (53 33, suite 22096) ainsi qu'à CARL JUNG (34 52, suite
22370).
Ce pourrait encore être ACHT SECHS (ou 8 6), 32 54 = 86, nombres de la série Bleue du Modulor. J'ai déjà dit la navrante débilité de ce système. Tout le monde ne mesure pas 183 cm, et on ne verra jamais Victor Wembanyama s'aventurer dans la Cité Radieuse du fada. Je l'ai visitée et ai éprouvé une terrible sensation d'oppression alors que je ne mesure que 170 cm.
Une de mes absolues sidérations a été un des premiers Thilliez,
La forêt des ombres (2006), véritable compil des nombres de la série Bleue (32-54-86-140-226), comme le sera
Labyrinthes (2022) pour les Fibos.
Il y sévit
le "BOURREAU 125" (101+125=226), de son vrai nom ARTHUR DOFFRE (86+54=140). Il a pour complice EMMA (=32), laquelle psalmodie cette suite de chiffres en allemand
neun... acht... sieben... acht... vier...NEUN ACHT SIEBEN ACHT VIER = 54+32+54+32+54 = 226
soit la longueur exacte en cm de l'instrument Modulor, ruban gradué avec
les séries rouge et bleue
Ce croquis de Le Corbusier est supposé montrer l'adéquation de
son système avec les postures courantes d'un homme, pourvu qu'il mesure 6
pieds ou 183 cm, à partir des briques 16 et 27 de la série Rouge, équivalents de 32 et 54 dans la série Bleue:
Un nombre essentiel apparaît à la fin du roman, 97878. Enuméré en chiffres allemands comme plus haut, ce serait
NEUN SIEBEN ACHT SIEBEN ACHT = 54+54+32+54+32 = 226
J'était plutôt certain qu'il y avait une intention là-dessous, qui ne l'aurait été? D'autant que les allusions explicites au nombre d'or et à Fibonacci sont nombreuses chez Thilliez; on y trouve même des personnages nommés Corbusier et Fibonacci.
La réelle sidération est venue lorsque j'ai
appris que, dans les deux premières éditions du roman, on ne trouvait pas
neun... acht... sieben... acht... vier...mais
neun... archt... sieben... archt... vier...grossière erreur, répétée, annihilant tout un pan de la construction envisagée autour de la série Bleue.
Puisqu'il est beaucoup question de "vérité", les seules "vraies" mesures du Modulor original étaient 226 cm de la série Bleue et 113 cm de la série Rouge, choisies pour leur proximité avec 89 pouces et 89 demi-pouces.
Je rappelle VERITAS = 89 (alphabet latin)
Il y a quelque temps, j'ai acheté un ruban Modulor pour voir ce qu'il en était, mais il s'agit maintenant d'un outil adapté au système anglo-saxon, mesurant exactement 89 pouces.
9 mars
J'accélère la cadence, peu sûr du temps qu'il me reste.
Je rappelle que chaque chiffre du PostId 4440256918605723090 de ce billet 444 débuté le 28/2 est dû au hasard,et que j'ai été amené à y voir:
444 évidemment;
0256 = 4.4.4.4;
puis 02 avec un retour en arrière pour le 2 mars où j'ai repris l'écriture
5691 pour Marina Sloty ou Tania Vläsi;
86 pour Carl Jung, merle or, ou
acht sechs. [Ajout ultérieur: et évidemment VERTIGE]
reste 05723090, 3090 m'est immédiatement significatif, et reste donc en fait 0 5 7 2.
Peut-être 0 doit-il être compris comme "zéro", en rapport avec le cousin de Lavarède qui, après s'être vu en "triple zéro", devient le Corsaire Triplex (192="zéro+zéro+zéro"). C'est un souvenir très lointain que je ne peux mieux cerner.
En tout cas 2-5-7 m'évoque la suite évangélique dont il a été très récemment question dans ce billet et les suivants. Le nombre 257 m'est aussi significatif, notamment en tant que valeur de
THE GREEK COFFIN MYSTERY, voir plusieurs articles concernés, mais ce n'est que devant ce problème de compréhension de 0 5 7 2 qu'il m'est venu de retourner 257 en 752, nombre de vers des 9 premières églogues de Virgile.
Curiosité, il y a 10 églogues, mais
le site des Belles-Lettres parle de 9, ces 9 premières vraisemblablement, car la 10 est particulière, mais elle est évidemment présente dans le recueil..
J'ai réussi grâce à JiBé Pouy à publier mes découvertes sur Virgile sous forme d'un genre de polar, où tout ce que je disais sur Virgile était rigoureusement exact, et si extraordinaire que j'imaginais comme Roussel que ç'allait me valoir une gloire immédiate.
Ce ne fut pas le cas, et seul Vfois4 (Willy Wauquaire, prof de maths sup) vérifia mes calculs et s'en enthousiasma. Qu'il soit loué!
Tout n'était en fait pas rigoureusement exact, mais je n'appris que bien des années plus tard que l'outrecuidant E. De Saint Denis, responsable de l'établissement du texte, y avait oublié un mot. Bien des relations essentielles n'en dépendaient cependant pas, et la possibilité d'erreurs entrait dans mes argumentations. L'erreur, c'est le système dans l'Eugénie, comme disait mon trisaïeul (Napo 3).
Bref, voici ce que je disais de 752, nombre de vers des 9 premières églogues:
Il y a maintenant 15 ans j'imaginais un schéma numérique quaternaire des
9 premières Bucoliques de Virgile, dont l'architecture symétrique
autour de l'églogue centrale 5 avait déjà été remarquée. Mon idée
s'appuyait sur une formule de cette églogue centrale: En quattuor aras : ecce duas tibi, Daphni, duas altaria Phoebo.
Voici quatre autels, deux pour Daphnis, deux pour Phébus.
Le
Daphnis honoré dans cette églogue de 90 vers serait Caesar, dont la
valeur numérique en latin est 45. Deux autels pour Caesar = 90.
Phébus est un autre nom d'Apollon, dont le vocatif grec a pour valeur
numérique 331. Deux autels pour Apollon = 662, et les 8 autres églogues
totalisent 662 vers.
Il y eut un rebond quasiment concomitant. J'avais repris contact récemment avec Phrère Laurent, Laurent Cluzel pour ne pas le nommer, souvent cité dans les billets d'il y a quelques années.
Ceci a donné lieu à un échange dans les commentaires du post
Vérité d'évangile.
C'était le 441
e billet de
Quaternité, 441 valeur de l'hébreu
אמת,
emeth,
"vérité", et j'y rappelais en introduction la légende du golem, selon laquelle cette statue de glaise prend
vie par l'inscription sur elle de ces trois lettres. Pour la désactiver,
il suffit d'effacer la première lettre, réduisant l'inscription aux
deux lettres
מת,
meth, "mort", de valeur 440.
Dans son premier
commentaire, Laurent émet quelque chose qui m'a été incompréhensible:
HOLM KAAR = 79 ( via la poterie du vieil EMETH = vérité)
Je lui ai demandé des explications par mèl. Laurent était autrefois concepteur de jeux de rôle:
HOLM, KAAR sont les deux titres de deux de mes jeux vidéo. Respectivement écrit en 1996 et 1998.
HOLM, humain en langage lutin.
C'est l'histoire de Steeve, un jeune garçon qui va voler une poterie ancienne, gravée de runes (en lutin).
Elle était en possession d'un vieil érudit, EMETH (je ne savais pas que c'était le mot vérité).
Steeve a appris qu'une légende dit que les runes de la poterie sont une clé pour ouvrir la porte d'un univers parallèle. Le pentacle de passage est Stonehenge et aussitôt son larcin réussi, il file tester l'incantation sur le site.
Il se retrouve dans un monde type faerie, où des lutins subissent les assauts des forces des ténèbres menées par un hobgobelin , KAAR ( nom qui deviendra le titre d'un second jeu qui n'a rien à voir).
L'arrivée de Steeve bouleverse le monde des lutins.
Leur héros grièvement blessé, OHP, se retrouve dans notre réalité à la place de Steeve qui se retrousve devant YHZ, un puissant magicien, au chevet de son frère OHP.... Steeve , renommé HOLM pour les lutins, doit aller délivrer le plus jeune des trois frères, AHB, aux main de KAAR....
Principe de monde miroir humain = lutin
STEEVE = OHP
EMETH = YHZ
KAAR, nom du chef des forces obscures, est aussi le titre d'un second jeu, ici le nom de planète terre dans des dizaines de milliers.
L'axe de la terre est orienté vers le soleil, une face est gelée et l'autre brûlée, la zone de l'équateur est une immense sponge où des races humanoïdes s'affrontent, les rescapés humain d'un station spatiale tentent de survivre du côté obscur gelé....Un mèl du même jour était posté à
07:52: (avatar du - 0572 - du Post Id)
Il avait calculé la valeur 441 (
emeth, "vérité") du jour de naissance de sa femme exprimé en toutes lettres, et le sien donnant 446. Il ne pouvait savoir que, si 440 est la valeur de l'adjectif
meth, "mort",
446 est celle du substantif
maweth, "mort".
11 mars (ou 3/11 à l'américaine)
- 3090 - J'avais annoncé q
ue les 4 derniers chiffres du Post Id m'étaient significatifs, et ils m'évoquent aussitôt JEAN LAHOUGUE = 30 90.
J'ai repris contact il y a deux jours avec Jean, dont je ne savais pas s'il était encore en vie, et m'aperçois avec stupeur que ce 9 mars était le
09-03 !!! !!!!!!!!!
Jean est pour moi l'auteur de plusieurs des meilleurs textes à contrainte en notre langue. Il a de plus écrit deux romans inédits dont je suis l'un des dépositaires,
Le regard et
Genèse, mais hélas son caractère disons "entier" n'a pas facilité jusqu'ici leur édition. Je crois pouvoir annoncer qu'il est aujourd'hui prêt à quelques concessions, avis aux amateurs!
J'ai récemment été amené à étudier les concaténations prénom-nom, telle Elisabeth Lovendale devenant 8190.
Considérer JEAN LAHOUGUE = 3090 m'a ainsi fait voir que 3090 vaut 5 fois 618, un nombre évocateur pour les fondus du nombre d'or (618/1000 ≈ 1000/1618), et reprendre ma collection de Lahougue m'a fait tomber sur ce bandeau, du temps où les grandes surfaces accordaient encore une réduction de 5% sur les livres:
Voilà.
Quaternité c'est fini. Pourtant c'était le blog de mon premier amour.
Je déplore de laisser en plan diverses choses que je pensais ajouter au billet 443, mais j'en ai marre.
Il reste quelques scories inutilisées ci-après, peut-être cela pourra-t-il aider les chercheurs...
----
Et il y a qqch que j'avais oublié et qui relance complètement la "vérité" chez Thilliez.
Ce sont 2 des 444 posts du blog, et ça me désole que tout ça risque d'être perdu avec moi, à cause de ma timidité et de ma difficulté à communiquer, alors que ça va bien plus loin qu'une théorie de plus. Il s'agit de l'âme du monde...
----
APRIL ORENSKI = 56/91
https://quaternite.blogspot.com/2013/02/
LUCAS / JOUBERT = 56/91
http://quaternite.blogspot.com/2013/02/seraphita.html
LUCAS / ilan (hébreu)
https://quaternite.blogspot.com/2016/08/puzzle-pour-fous.html
.PNG)
